边缘检测算法分析
背景
边缘检测是图像分析中使用到的最常见的操作之一,边缘增强(edge enhancement)和边缘检测(edge detection)相关的算法可能是最多的。
这里对边缘检测算法做个大致的分析。
边缘检测基本概念
1.目的
从广义上来说,其原因在于边缘形成了一个对象的轮廓。对象是图像分析和视觉系统中重要的处理主体。边缘是对象和背景之间的边界,还能表示重叠对象之间的边界。
这意味着,如果图像中的边缘可以准确地被识别出来,那么所有的对象都可以被定位,而且对象的基本属性(例如面积、周长和形状)都可以被测量出来。
由于计算机视觉要涉及图像中对象的识别和分类,因此边缘检测成了一个基本工具。
注意,无法判断图像中哪一部分为背景、哪一部分为对象,只能识别出各个区域之间的边界。
边缘检测被称作图像分割(segmentation)的过程的一部分——图像分割的目的是识别出图像中的区域(region)
2.边缘检测与边缘增强
从技术上说,边缘检测是定位边缘像素的过程,而边缘增强是增加边缘与背景之间的对比度以便能够更清楚的看清边缘的过程。
在实践中,这两种术语经常互换使用,因为大部分边缘检测程序也会把边缘像素的值设置为特定的灰阶或颜色,使得边缘更容易被识别。
3.边缘跟踪
边缘跟踪(edge tracing)是沿着边缘进行跟踪的过程,这个过程通常会把边缘像素采集到一个列表中。这个过程以一个一致的方向进行,既可以顺时针,也可以逆时针绕着对象旋转。
链码算法(Chain coding)是边缘跟踪算法的一个特例。这种算法得到的结果是对象的一个非光栅表示,可以用于计算形状测量,或者对对象进行识别或分类。
4.经典的边缘检测算法
经典的两种边缘检测算法是:Canny边缘检测器和Shen-Castan边缘检测器(也称作ISEF边缘检测器)。
这两种检测器都有坚实的理论基础,而且都声称具有一定程度的最优性;也就是说,这两种检测器都在特定的场景下可以达到最好效果。
具体这两种检测算法,可以看后续blog
传统的方法与理论
1.理论
大部分好的算法都会事先声明清楚能够解决的问题,并且的都会对解决问题的方法以及方法能够正确工作的条件进行有说服力的的分析。
在这个框架基础下,要定义一个的边缘检测算法意味着首先要定义什么是边缘,然后利用这个定义提出边缘增强和边缘识别应该采用的方法。
2.理想阶梯型边缘
边缘可能有多种定义,每一种定义都适用于某些特定的场合。
理想阶梯型边缘(ideal step edge)是一种最常用也最有一般性的定义。如下图所示: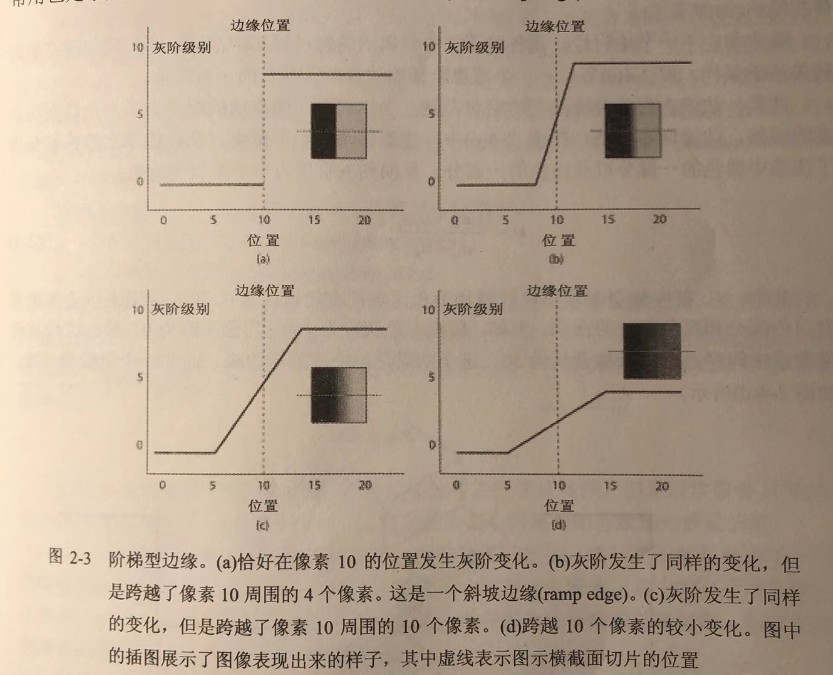
这里看出,边缘只不过是在某个位置发生的灰阶变化。
灰阶变化越大,边缘的检测也就越容易(不过在理想的情况下,任何灰阶变化都可以很容易地看出来)。
3.边缘检测的难点
边缘检测的难点主要有两个:
(1)第一个难点来自于数码化。
图像的采样不可能使得整个边缘刚好落在像素边界上。事实上,灰阶的变化可能遍及多个像素(如图2-3的(b)~(d)所示)。
可以认为边缘的实际位置在连接低灰阶与高灰阶的斜坡(ramp)中央。这个斜坡只是数学意义上的斜坡,因为在图像数码化(采样)之后,这个斜坡实际上呈现的是阶梯锯齿状。
(2)第二个难点来自于无处不在的噪声问题。
由于受到很多因素的影响,例如光强度、相机和镜头的类型、移动、温度、大气效应、粉尘和其他因素,因此在场景中表示同样灰阶的像素很可能在图像中不是同样的灰阶。噪声是一种随机效应,因此只能通过统计的方式特征化。
噪声对图像造成的结果是使得有些像素的灰阶值产生随机的变化,因此理想边缘中的平滑线条和斜坡在真实的图像中是不可能遇到的。
4.边缘的模型
在没有噪声的情况下,任何明显的灰阶变化都可以表示边缘。
在图像中几乎不可能真正遇到阶梯型边缘,因为:
(1)对象很少有如此清晰的轮廓;
(2)场景的采样永远都不会让边缘正好位于像素的边缘上;
(3)存在噪声
斜坡是一个模型,它表示为了产生台阶,边缘本应该是什么样子,因此这是一个理想化的情况,而实际上遇到的是数据插值的结果。
尽管理想的阶梯边缘和斜坡边缘模型在过去通常用来设计新的边缘检测器,但是这种模型是一种简化的模型。
5.噪声
任何图像获取的过程都可能会产生某种类型的噪声,因此忽略噪声是没有意义的。没有噪声的理想情况在实践中永远也不会发生。
由于噪声的随机本质,因此无法准确的对其进行预测,而且无法在一个有噪声的图像中准确测量噪声,因为无法区分噪声对灰阶的影响以及像素数据对灰阶的影响。
然而,有时候可以通过噪声对图像造成的效果来对噪声进行特征化。
噪声的特征通常可以用带有特定平均值(mean)和标准偏差(standard deviation)的概率分布来表示。
在图像分析中,特别关注的是以下两种类型的噪声:
(1)信号无关的噪声(signal-independent noise)
(2)信号相关的噪声(signal-dependent noise)
(1)信号无关的噪声
信号无关的噪声是一组随机的灰阶值,在统计意义上和图像数据无关,这些数据加入图像的像素中产生了带噪声的图像。
当一幅图像通过电信号的方式从一处传输到另一处的时候会产生这种噪声。
令A为完美图像,N为传输过程中产生的噪声,那么最终得到的图像B为: B = A + N
A和N互相没有关系。噪声图像N可能没有任何统计属性,但是通常假设N符合正态分布(高斯分布),其中平均值为0,标准偏差为某个测量到的值或者预先假设的值。


(2)信号相关的噪声
在这种情况下,图像中每一点的噪声值的大小为这一点灰阶值的函数。
一些照片中的颗粒就是这种噪声的例子,而这种噪声通常都比较难以处理。不过幸运的是,这种情况不是太重要,如果照片采样合适的话,这种情况也是可以处理的。
很难在各种不同的随机情形中都找到边缘,但是一个好的边缘检测器在这种情况下也应该能够判断边缘的位置。
边缘是由灰阶(或色彩)等高线定义的。穿过等高线的时候,灰阶值会迅速变化;沿着等高线走,灰阶值的变化会更加轻柔,有可能是随机变化。因此可以得出结论:边缘具有一个可测量的方向。
定位边缘
边缘像素和噪声像素都具有的特点是,相比周围像素有明显的灰阶变化。
而边缘像素互相连接,构成了等高线,因此可以通过这一个特性将边缘像素和噪声像素区分开来。
3种常见的算子可以用于定位边缘。
(1)导数算子
这种算子被设计为标识发生巨大强度变化的地方。
(2)类似于模板匹配的方案
其中边缘由一个很小的图像进行建模,这个图像表现出了完美边缘的抽象属性。
(3)使用边缘的数学模型
其中最好的也使用了噪声模型,并且努力吧噪声因素考虑进去。
这一种类型的算子,是我们主要需要关注的。
源码
给图片添加噪声的算法代码:
https://github.com/ThranduilELFKING/study-openCV/tree/main/makenoise
估计噪声的算法代码:
https://github.com/ThranduilELFKING/study-openCV/tree/main/measurenoise
